凸轮凹槽轨迹的数学处理及数值计算
根据凸轮的工作原理,我们知道凸轮的加工方法是要求铣刀模拟转盘上某一滚子的运动把凸轮上的曲线轨迹加工出来。由图3.6可以看出,一方面。滚子运动轨迹是半径为 的圆弧,而凸轮轴线与弦OS重合,这要求铣刀在 坐标平面上作圆弧插补运动,走出圆弧OG。为使刀具与滚子的轨迹相符,加工时刀具除沿S向(机床X轴方向)移动外,还必须沿轴线的法向(机床y轴方向)作补充位移。另一方面,曲线的升程要求一个余弦加速度运动曲线
这一运动可由凸轮随数控转盘的回转运动和铣刀沿 轴作的直线运动复合而成。这是,最好的办法是,只要求铣刀沿 轴作的直线运动,而将其在 坐标平面上作圆弧插补运动中的 向位移量迭加在凸轮的理论曲线轨迹上各点的 向位移上,即将其附加在凸轮随数控盘的回转运动中。这样,就可以把必须同时进行两种运动,从而得以在 数控铣床上把凸轮的凹槽轨迹加工出来。但是采用这种方法时,必须在编程前,对凸轮的理论曲线进行必要的修正。
(1)轨迹的修正方法 因滚子运动规律的推导,是将其运动轨迹放在凸轮展开平面内进行的,得到的是凸轮的理论曲线。由于加工时铣刀的 向补充运动,所以迭加后的曲线应该是实际凸轮曲线,即与理论曲线不重合的修正值曲线(见图3.6中的虚线)。其修正值 是一个变量,变化规律与OG弧的半径及凸轮的升程有关,根据图3.6,可得出轴线方向上任一点 处的修正值
升程 =55mm;滚子个数Z=18;滚子分布半径 =158.366mm。
把上述数值计算,得
(4-2)
根据式(4-2)计算出程编所需各节点 处的Y向修正量 后,再与凸轮的理论曲线上 处 坐标值相加,即可求得修正后的新节点坐标( , ),而这一组新点所构成的曲线就是凸轮加工后的实际轨迹。
(2)引导圆弧计算凸轮出入口处的导引圆弧R44及R96的程编节点坐标的计算可按弦线逼近法进行。对于圆弧,用弦所对应的夹角增量 更方便些,见图3.7。其方法 如下:
1)用公式设定的 (本例选 =0.02mm),分别计算出
为保证加工精度及计算方便,可只取整数部分,即 , ,再进行下一步计算;
2)按公式
(用于R96);
(用于R44)
分别计算出各节点的绝对坐标值。
(3)节点计算 凸轮的理论曲线上各节点的坐标计算仍采用弦线逼近法。因该理论曲线要进行修正,故不采用前述的等插补段或等插补误差法进行,而按回转角的增量 来取节点。根据该凸轮加工精度及最小曲率半径等情况,本例取 来求得对应的X向(凸轮轴向)升程。
(4)编制坐标数据表 建立编程所用各节点坐标计算数据表,为编程作好充分准备,并作如下说明:
1)按图3.8建立的编程坐标系计算;
2) 为凸轮的理论曲线回转角(自变量);
图3.7圆弧节点坐标
3) 为修正量,按式(4—2)计算;
4)S为凸轮的理论曲线升程值,即轴向位移 ;
5)Y为节点的线性(展开后)绝对坐标值,以 算出, 为按回转角 算出的凸轮表面展开后的线性值,因其直径值为150,故, 也是展开后的线性值;
6)将线性展开的绝对坐标y转换为转盘的绝对转角A时,按式 计算;
7) 为入口R96圆弧段, 为R44圆弧段, ,为直线段, 为修正后的凸轮曲线段, 为直线段, 为出口R44圆弧段, 为R96出口圆弧段,与图3.8中一致;
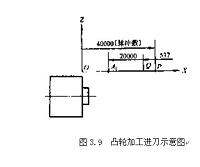
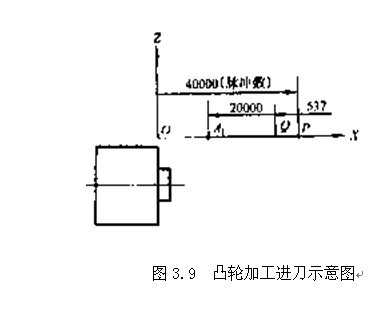
8)凸轮轨迹铣加工走刀路线
7.凸轮凹槽数控加工的程序编制
在程序编制中首先应处理好以下几个问题:
(1)计算误差由于在转角值、平面线性值的转化计算过程中,经常遇到非整除的情况,其舍、入误差积累过多将直接影响轴向总位移(升程) 的制造精度,并且也造成加工后铣刀中心不能完全回零。因此,编程时应设法将这种计算误差消除,为避免某些点上误差过大,不要集中在某个程序段中,而应采取分散处理的方法,一般来说,在(一个程序段中加减一个脉冲就可以了。此外,在编程后一定要把凸轮曲线段总位移的代数和求出,检查轴向(x)位移之和是否等于55mm,这时数控转盘的总转角 是否等于 ,再检查各坐标的位移代数和是否分别为零。
(2)切入切出量从铣削工艺来看,在人口处,刀具要在下刀后进人工件,应将人口处的圆弧向凸轮体外延伸出一个切人量,其轴向切入量应大于铣刀半径;在出口处也应有切出量,以便让铣刀完全走出工件。
(3)机床间隙对加工的影响 因该凸轮加工精度要求较高,特别是总导程( ),其允许误差只有±0.01mm,不消除机床的反向间隙,则难以保证加工质量,因机床本身的间隙补偿装置很难调到间隙为零的最佳状态,故只能利用编程技巧来进行修正,这里介绍反向进给法。先将刀具从原点出发,向x进给的反方向走一位移,然后将刀具再向进给方向位移运动,以达到对机床反向间隙作第一次“压紧”;接着再让刀具在下刀前向进给方向位移至下刀点。这样,通过两次“压紧”,间隙将被消除。由于从以后的程序起,直到加工完为止(铣刀走出凸轮体),铣刀X向运动方向一致,无反向运动,从而消除了机床反向间隙可能带来的加工误差。当铣刀返回原点时,反向间隙又被带入,为保证回零准确,并便于验证其重复定位精度,有把握的进行二次加工,故也应增加消除间隙回零的附加程序段,其方法同上一样。对于数控转盘的运动,也应进行相同的处理。