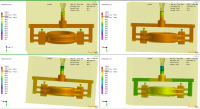
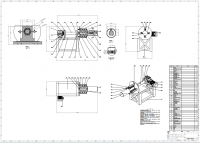
曲柄压力机工作机构的运动和受力分析设计
滑块的运动规律
曲柄压力机一般为曲柄连杆机构。则滑块的运动规律与曲柄连杆机构的运动规律相同。即滑块随连杆绕节点(曲轴或偏心轮)转动沿一直线作往复运动。
2.1.1 滑块的行程与曲柄转角的关系
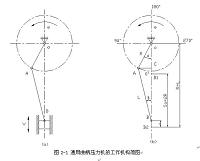
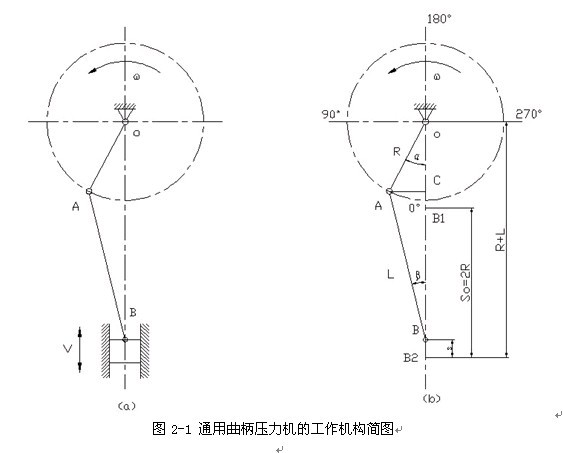
通用曲柄压力机的工作机构大多采用结点正置(滑块和连杆结点B的运动轨迹位于曲柄旋转中心O相连结点B的连线上)的曲柄滑块机构。图2-1(a)是曲柄、连杆和滑块的运动简图。图中O点为曲轴的旋转中心,A点为连杆与曲柄的连接点,B点为连杆与滑块的连接点,B1、B2点分别代表滑块的上死点和下死点。
图2-1 通用曲柄压力机的工作机构简图
曲柄压力机滑块是在接近行程下死点的一段区间工作,因此,在研究滑块运动规律时,取滑块行程的下死点B2为行程的起点,滑块从B2点到B点为滑块行程S。曲柄转角由A0点算起,相应顺时针方向(和实际转动方向相反)转到A点时,曲柄转角为α。
如图2-1(b)所示,当曲柄滑块机构处于0AB位置时,滑块的行程
式(2.1)
而
令
则
而
所以
则
式(2.2)
由于 一般小于0.3,对于通用压力机, 一般在0.1~0.2范围内,故式子可进行简化。根据二项式定理,取
代入式子,整理得:
式(2.3)
式中: ——滑块行程,从下死点算起,以下均同;
——曲柄转角,从下死点算路与曲柄旋转方向相反者为正;
R——曲柄半径;
——连杆系数;
L——连杆长度(当连杆长度可调时取最短时数值)。
因此, 已知曲柄半径R和连杆系数 时,侄可从式中求出对应于不同的 角的S值。
2.1.2 滑块的速度和曲柄转角的关系
求出滑块的位移与曲柄转角的关系后,将位移S对时间t求导数就可得到滑块的速度v,即:
式(2.4)
而
所以
式中 ——滑块速度;
——曲柄的角速度。
又
则
式(2.5)
式中 n——曲柄的每分钟转数,亦即滑块每分钟行程次数。
2.1.3 滑块的加速度和曲柄转角的关系
对于高速压力机,滑块运动的惯性力必需予以足够注意。为此,需要求出滑块的加速度和曲柄转角的关系,将上式对时间求导数即得:
式(2.6)
式中 ——滑块加速度。
由JH31-315压力机的行程S=315 mm,连杆长度L=1588 mm,偏心轮转速n=20转/min,
则
mm 式(2.7)
式(2.8)
代入以上公式,得运动数据表如下:
表2-1 运动数据表
0 10 20 30 40
0 0.0167 0.0662 0.1465 0.2547
0 2.63 10.4265 23.074 40.115
0 0.1911 0.3742 0.5433 0.6922
0 63.206 123.767 179.6965 228.945
续表2-1
50 60 70 80 90
0.3865 0.5375 0.7022 0.8748 1.0500
60.87 84.656 110.5965 137.7810 165.375
0.8152 0.9093 0.9722 1.0022 1
269.627 300.75 321.555 331.4776 330.75
2.2 曲柄滑块机构的受力分析
图2-2为结点正置的曲柄滑块机构滑块的受力简图。滑块上受到工件变形抗力P的作用,在忽略摩擦力的情况下,P力由连杆上给予滑块的作用力 及导轨给予滑块上的反作用力Q相平衡。根据力的平衡原理得:
式(2.9)
式(2.10)
由前推导得知, ,若 =0.3,当 时, =0 。当 = 时, ,在通常情况下,特别是对通用压力机, 远小于0.3,故 远小于 。由于 角较小,因此,可以认为 , ,故上述二式写成:
式(2.11)
式(2.12)